前面我們講了費茨定律的理論內容,如果你認真消化后應該對費茨定律在研究什么,以及影響指點事件效率的關鍵因素已經有所了解了。(回顧: 《費茨定律》)
為了讓費茨定律更易于理解,今天我挑選了一些案例并加以總結,希望用真實的場景幫助你打開一些實操設計的思路。
前情提要:費茨定律指“指點 動作消耗的時間T與 距目標離D成正比,與 目標大小W成反比。
一、費茨定律的常規思路
① 從距離切入的常規使用
1.1 對于起始點明確的指點事件
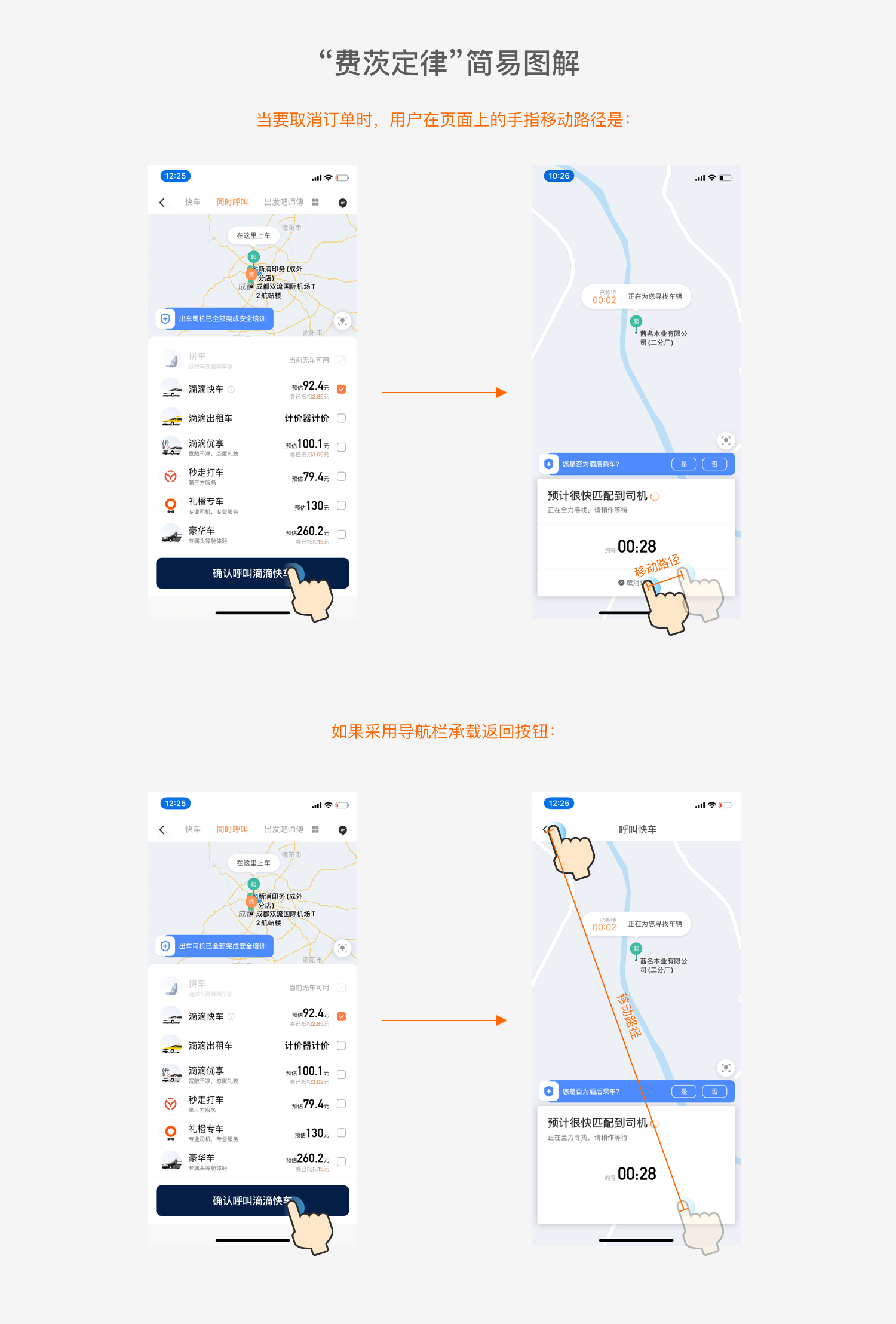
以前我在UI控件專題中分析導航欄使用方法的時候,有引用過滴滴的案例,談到了我對滴滴的“取消訂單”操作交互設計的看法,當時是 將該操作與使用常規導航欄取消訂單進行了對比。
首先毋庸置疑,「取消訂單」對于業務方來說是一項 負向情緒操作(即:與業務流程、商業目標相悖的操作)。我們在日常設計界面與交互時,總是希望避免用戶產生負向情緒操作,這一點對于久經沙場,常與產品、運營甚至老板對接的設計師朋友,應該能夠達成共識。
所以我們看到滴滴對于「取消訂單」操作采用了費茨定律中的 減小目標區域大小W的設計,將「取消訂單」按鈕設計得 小而不顯眼。
但盡管我們總是在極力避免用戶負向情緒操作,可也無法徹底規避特殊場景的產生。例如示例中,滴滴雖不希望用戶取消訂單,但依然無法規避用戶誤操作呼叫、等待時間過長等場景而導致需要取消訂單的行為。
從上圖中很容易看到,當用戶點擊「確認呼叫」時, 點擊「確認呼叫」按鈕是一個起始點明確的指點事件,與「取消訂單」的間距很小。對于有明確取消訂單意愿的用戶,可以快速方便地進行取消呼叫操作。
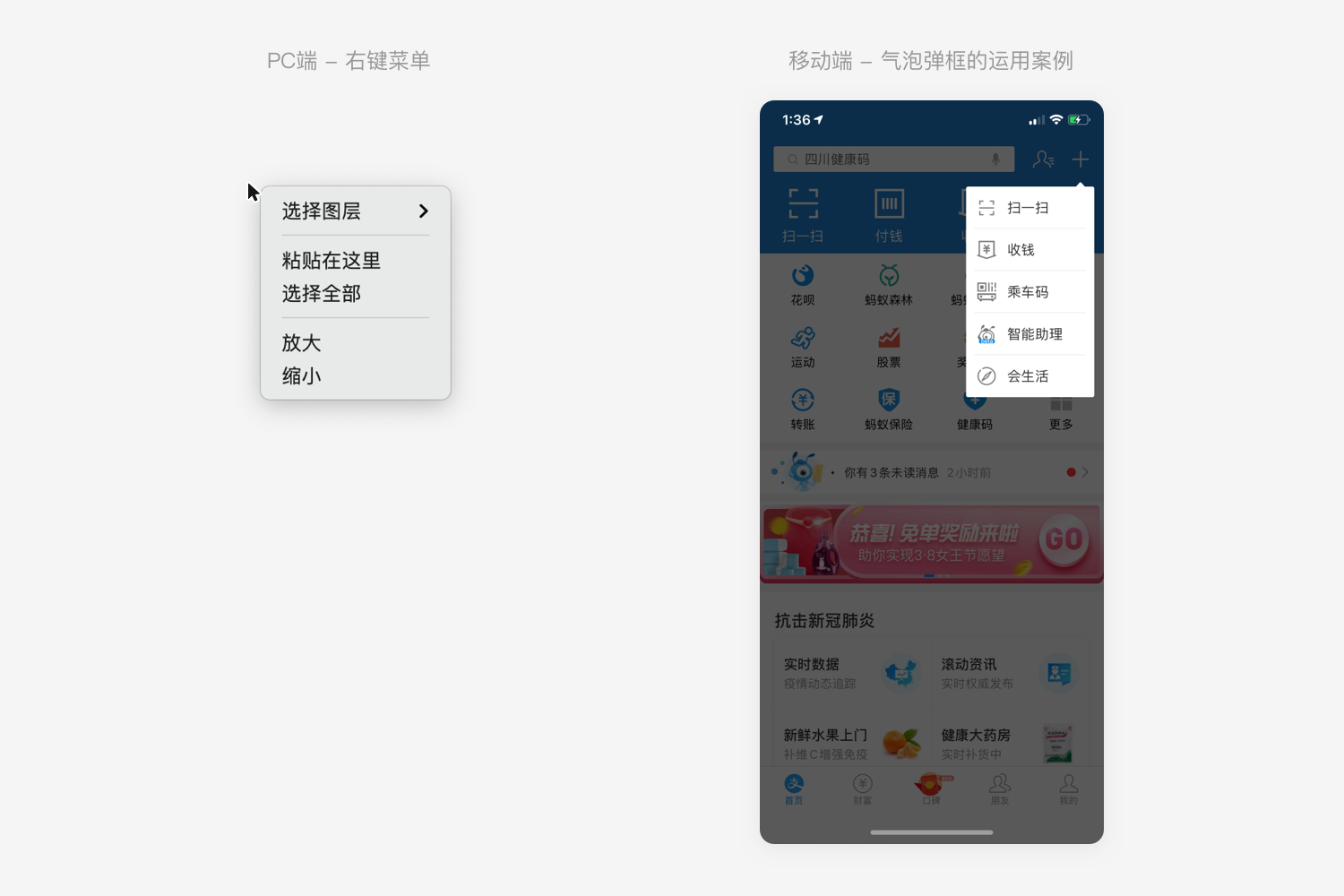
再例如PC端中,我們在任意位置點鼠標右鍵,都會在 當前位置彈出右鍵菜單。點擊鼠標的位置是明確的起始點,在就近位置彈出菜單可以大大降低目標與起始位置的距離。
主流移動端規范中,iOS與Material Design的氣泡彈窗菜單,也和PC端右鍵菜單的設計有異曲同工之妙,在許多APP中也屢見不鮮。
?設計思想總結
分析當前設計場景中的功能與前后步驟是否有(關鍵)聯動關系。如果有,即可以將功能入口定義為起始點明確的指點事件。如果聯動關系具有正向意義,請進行思考,是否采用減小目標區域距離D的設計,來協助提高用戶操作效率。
1.2 滿足操作習慣的指點事件
有聯動關系的功能場景其實是非常具體的,具體的案例當然比較少見,而抽象的場景其實才占據了我們設計需求中的絕大多數。 有時候一個頁面的功能繁多,我們無法具體弄清楚用戶到底想要做什么。
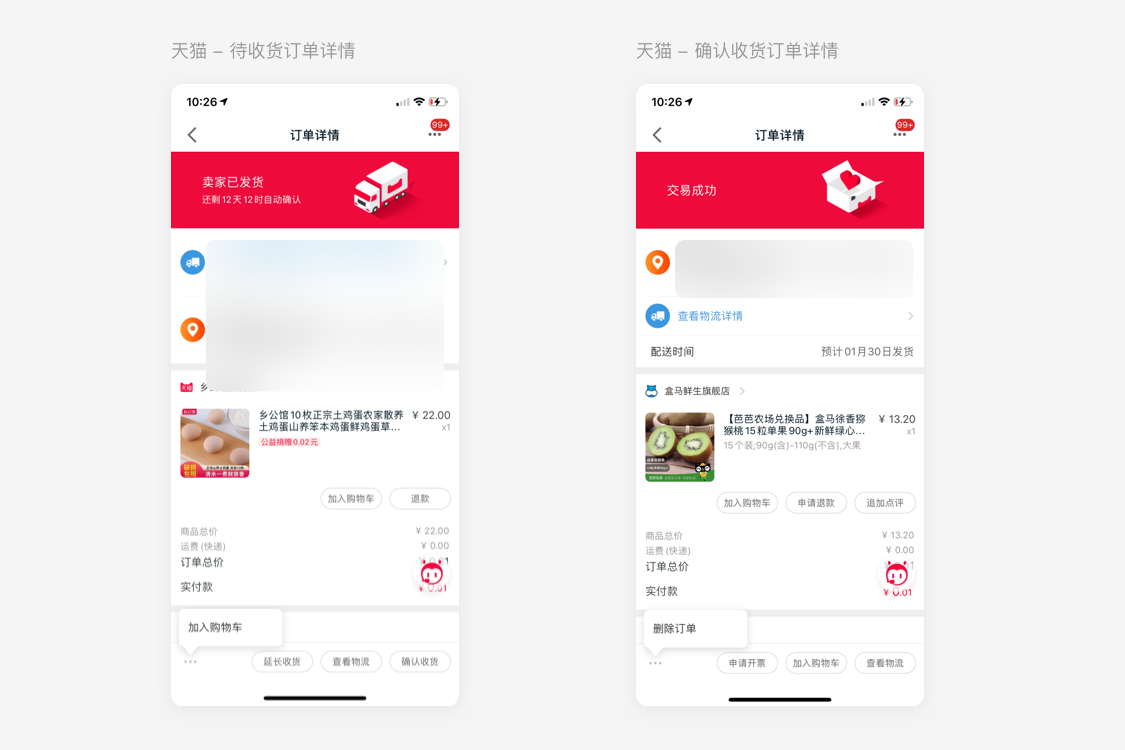
舉個例子,當用戶點開一個電商歷史訂單,他想要做什么呢?查看物流、查看訂單號、評價、復購、聯系售后?可選擇性太多。我們無法確定用戶究竟想干嘛。
頁面中的信息與功能非常多,且不同的訂單狀態設計到的功能展示也各不相同。但滑動頁面時,始終有幾個關鍵操作 被固定在頁面底部,并且居右排列。
和前面起始點明確的操作相比,我們的設計需求可能包含太多不能完全明確起始點的指點事件,但為了幫助用戶做出選擇,我們可以 盡量使關鍵指點動作符合當前設備的操作習慣。
例如手機這樣的小屏設備,我們拇指最常操作的區域就是屏幕的右側中下部,拇指時常是停留在這個操作區域的,所以將主要功能操作放置在設備中下部, 雖然不能明確起始點,但可以盡可能減小操作的移動距離。
?設計思想總結
面臨“一個頁面不只做一件事”的情況,要 幫助用戶梳理繁多功能點中的功能優先級和操作頻次數據,優先級高、頻次高的操作可以結合當前操作設備的操作習慣,協助提高用戶操作效率。例如:當設計車載HMI時,我們是否可以考慮將司機高頻功能,如廣播、導航等置于偏主駕駛座方,方便司機操作;而次要功能可以放置于偏副駕駛座方。
② 從尺寸切入的常規使用
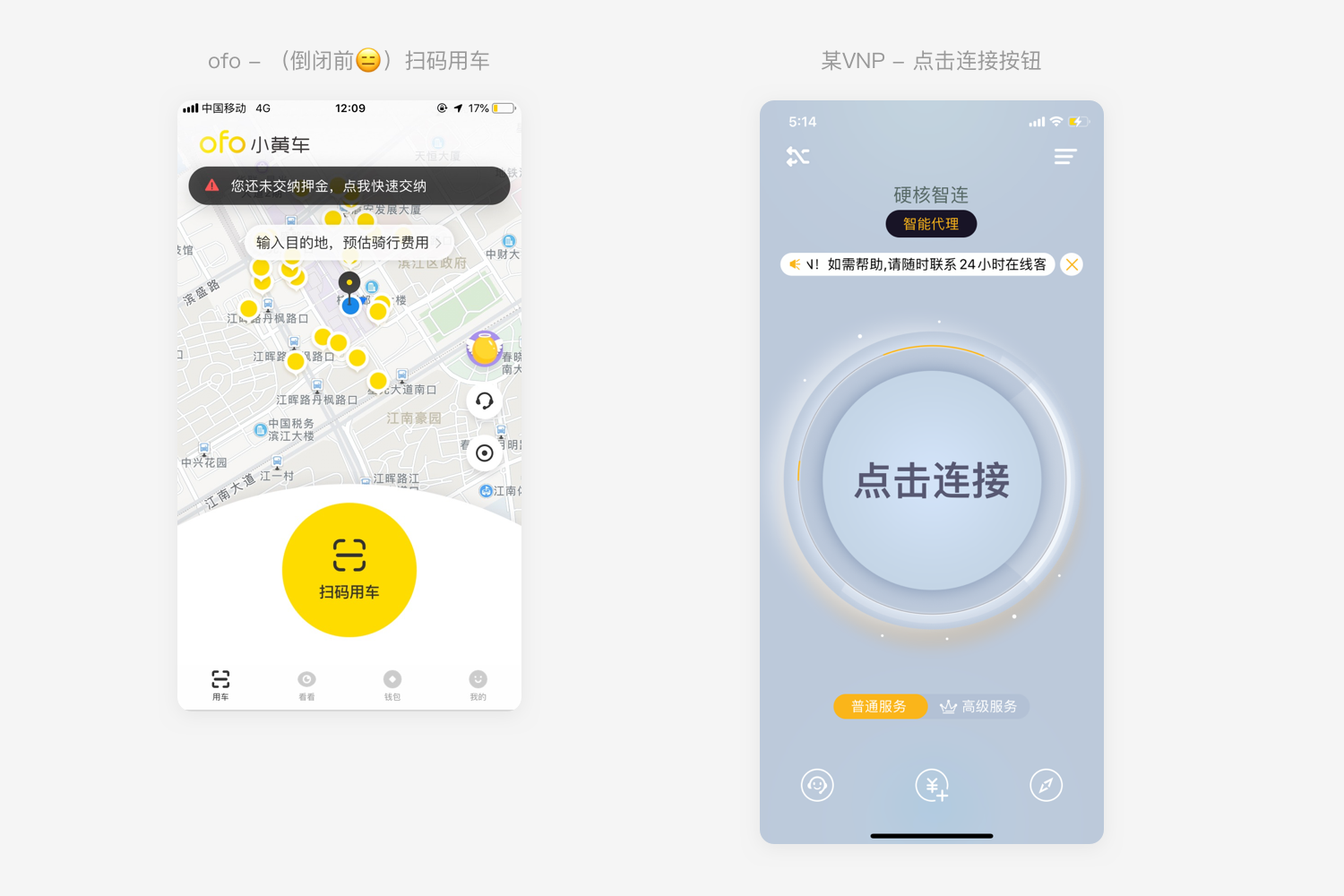
2.1 簡單粗暴地放大按鈕尺寸
對于功能點比較單一、頁面內容比較簡單的頁面, 放大按鈕的尺寸一方面能夠填充頁面內容,同時也可以利于用戶點擊。
2.2 擴大操作熱區
考慮到平衡視覺關系,我們可能無法為了提高用戶操作體驗,而在頁面中將每一個操作都簡單粗暴地放大。但我們可以選擇 在元素視覺大小不變的情況下,擴大觸發操作的范圍,即擴大熱區。
?設計思想總結
擴大事件響應區域是我認為提升指點效率最粗暴也是最有效的方法(還記得上一篇文章我提起的“指墻”的例子嗎)。對于擴大指點區域, 我們可以根據頁面具體內容排版,往兩個方向思考:①直接擴大視覺元素;②保持視覺元素不變,擴大響應熱區。兩個方案分別是從UI和前端落地上切入,所以要記得有效溝通。
二、費茨定律的反向使用
以上我們所講到的案例,都是通過正向思考產生的。但許多交互與UI設計中,反向思考、逆向使用費茨定律的例子,也不在少數。
這很好理解, 當我們不希望讓用戶過于方便地操作的時候,我們就可以開始進行逆向思維,反向使用費茨定律,增加用戶的操作難度。什么時候我們不希望用戶過于方便地操作呢?—— 重要或危險操作需要用戶小心謹慎,或者壓根想阻撓用戶操作的時候。
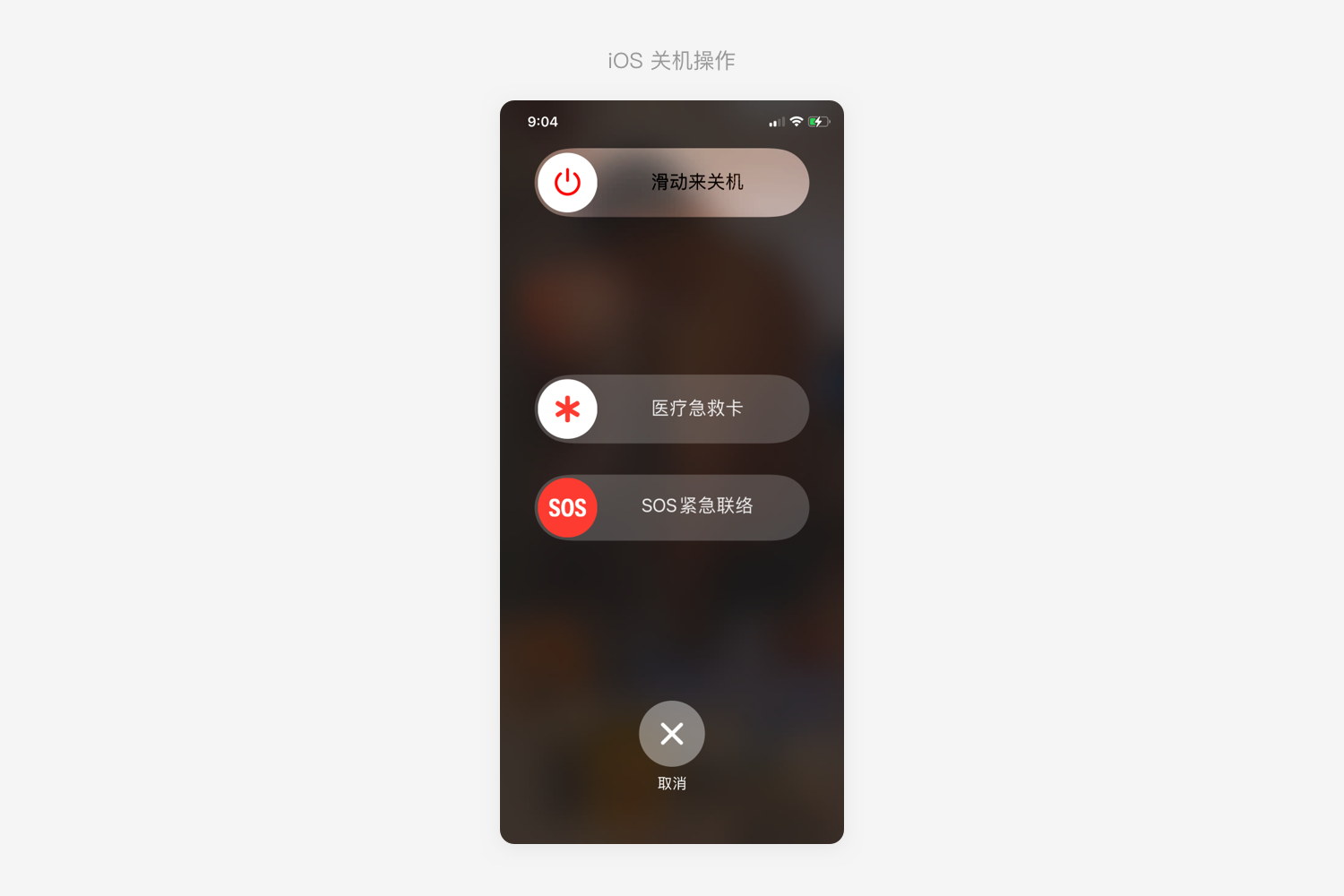
反向使用費茨定律最常被人引用的案例就是iOS的關機操作。
iOS的確認關機操作居于設備的頂部區域,是不太滿足用戶對手機的操作習慣的。其次通過滑動關機操作也增加了費茨定律中的「距離D」。各種反向設計都是為了提高用戶操作的不便性,放置用戶誤操作。
同時費茨定律的反向使用方法在一些商業需求中也經常被使用。
我們常常看到許多商業廣告的關閉按鈕被設計得很小,且點擊區域也和用戶習慣相悖,這也是反向使用費茨定律的案例。雖然從用戶體驗上來說,我們都希望盡量避免這些設計存在,但在商業價值面前,你懂的。
三、寫在最后
最后我想再回到費茨定律的公式 T=a+blog2(D/W+1) 談一談對于設計法則的看法。
對高中數學還有一些記憶的朋友,應該對log函數不陌生,是求冪的逆運算。 log函數往往會大幅抵消真數變化對底數的影響。我舉個具體數值的例子:
我們如果簡單記為T=log2(D/W),假設「距離D」是「大小W」的32倍,那么T=log2(32)=5。如果保持「大小W」不變,「距離D」縮小為原來的1/4,即「距離D」是「大小W」的8倍,那么T=log2(8)=3。
看到了嗎,「距離D」雖然縮小了4倍,但因為log函數的影響,T縮小的倍數還不到原來的1/2。何況 我們在移動設備交互設計中,時間T往往連一個整數秒都達不到,通常是毫秒級的,所以就算「距離D」與「大小W」比率成倍變化,對時間T最后的真實數值改變其實非常微小。
在對費茨定律的講解結束之際,我講這個是為了說明了什么呢?
我相信讀者中,抱有“其實這樣做和那樣做,最后的實質性差別并不大嘛”想法的大有人在,但對于老前輩們寫進書里的理論又羞于反駁。起初我時常和你們一樣。
但隨著做設計的時長越長,慢慢發現, 多看多學“法則”其實往往是在鞏固一種思維模式和思考 方向,而這些我們裝在腦中的 東西往往比法則本身更有價值。對于費茨定律我希望大家不要像我起初抱著絕對的數學思想去理解,不然會走進一個胡同。多用開放思維去理解,可能更容易打開你設計的思想和對設計的理解~